前回の記事で、3群以上の対応のあるノンパラメトリックデータに関して有意性を検定する方法であるフリードマンFriedmanの検定について説明しました。
今回はそれに合わせて押さえておきたい、3群以上の対応のあるノンパラメトリックデータに関して有意性を検定するKruskal Wallis(クラスカル・ワリス)検定をエクセルで求める方法に関して説明していきます。
Kruskal Wallis(クラスカル・ワリス)の検定
Kruskal Wallis(クラスカル・ワリス)検定は、対応のないノンパラメトリックデータに使用するものです。
このようなデータを多重比較する場合、通常はノンパラメトリック版Tukey法ともいえるSteel-Dwass法を用いる場合が多いですが、「それぞれのデータをマン・ホイットニーのU検定で検定、その後ホルムなどで多重比較したい!」という方向け(おそらく有意差がうまく出ない場合などに使いたい方)に説明していきます。
では実際に例のごとく適当なデータを作成して算出していきます。
データ群はA,B,Cの3群、測定回数はN=5,4,3でやってみます。
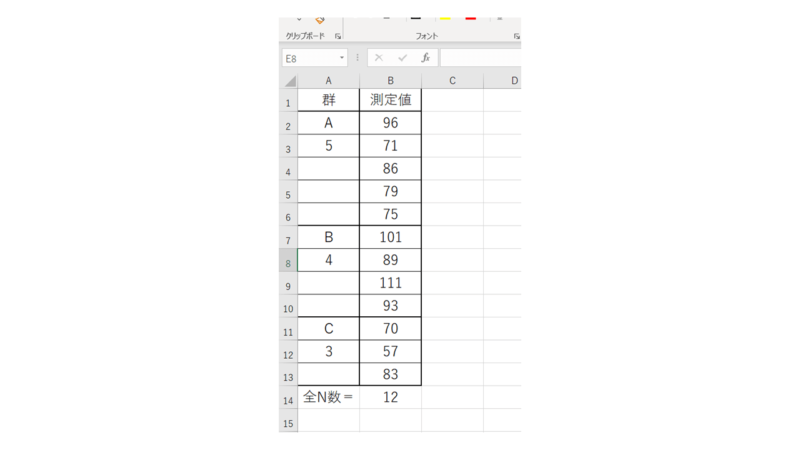
この手法では前回と違い、群を縦に並べておくと処理しやすいと思います。
各群のN数と全N数も計算に使用しますので先に入れておきます。
まずはノンパラメトリック検定でおなじみ、順位付けをします。
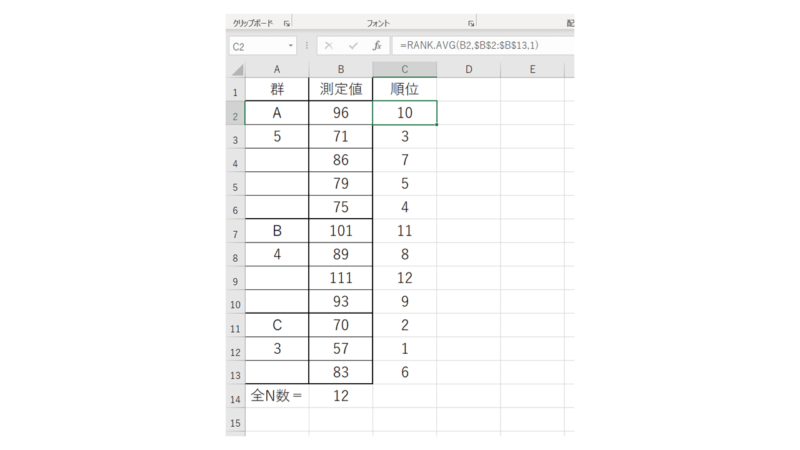
フリードマン検定と異なり、順位付けはすべてのデータに対し、まとめて行います。
こんな感じですね。RANK関数でやってしまいましょう。
※同順位値が出たら以前の記事でも書いたように、それ用の処理をしてください。
それぞれの群(A,B,C)の順位の値を平均します。
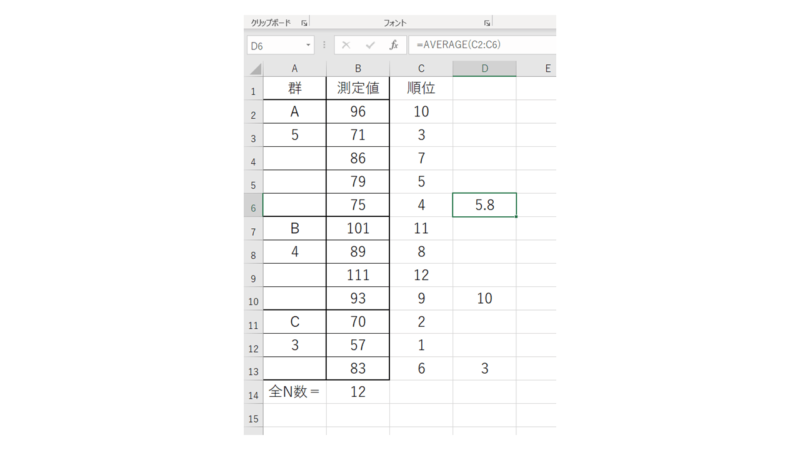
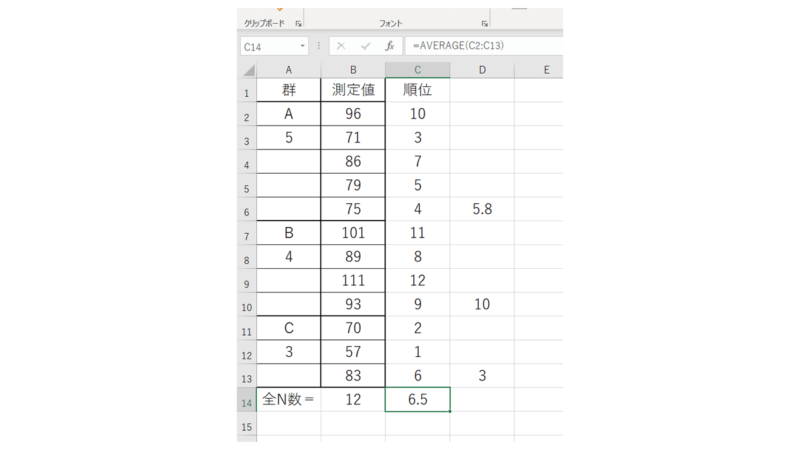
そして、全データの順位の平均値も算出します。
これを基に,クラスカル・ワリスの統計量Tを算出していきます。
かなり長いので、参照箇所を間違えないようにしましょう。

=12/(B14*(B14+1))*((A3*((D6-C14)^2))+(A8*((D10-C14)^2))+(A12*((D13-C14)^2)))
簡単に式の説明をしますと、全N数と全N数+1をかけたもの、各郡N数に各郡平均から全体平均を引いて2乗したものを掛け合わせて、それぞれ足し合わせたもの。といった感じです。
※注意点として、この式の最初の「12」は、どのようなデータでも「12」を用います。参照値ではありません。
統計量T=6.78462になりました。
統計量Tからp値を算出します。自由度は「2」ですね。
=CHIDIST(B15,2)
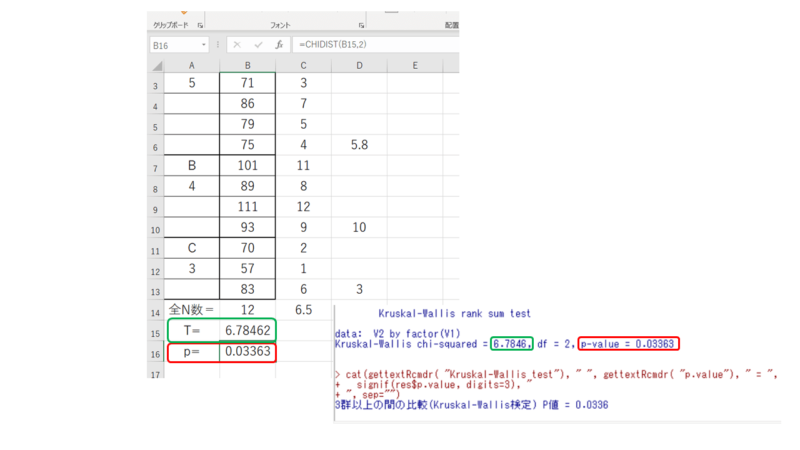
p=0.03363なので今回のデータ、3群間は有意性が認められました。
毎度確認に使っている統計ソフトEZRでも算出結果は同じになっているので問題なさそうです。
今回のデータについてデータ群間に有意性が認められたことはわかりましたが、ではどの群間に差があるのかを確認するには2群間のノンパラメトリック検定を行なわなければなりません。
今回のように対応のない2群間の検定にはマン・ホイットニーのU検定などを用いて、そこからさらに多重比較検定といった流れになります。
多重比較検定に関して、ボンフェローニについては以前少し述べましたが、その他の多重比較検定に関しても、後日記事にしていくつもりです。
3群以上の対応のないノンパラメトリックにはクラスカル・ワリスの検定!
今回、3群以上の対応のないノンパラメトリックデータの有意性を検定する方法であるクラスカル・ワリスの検定をエクセルで算出する方法に関して説明しました。
同じ3群以上のデータでも対応がある、対応がない、パラメトリック、ノンパラメトリック、それぞれにおいて有意性を確認した後に多重比較検定をする必要があります。
自分の扱っているデータに合った検定を行うよう心がけましょう。



コメント