以前の記事で、3群以上のパラメトリックデータに関して有意性を検定する方法でよく用いられるテューキーTukey法をエクセルで算出する方法を記事にしました。
今回はテューキーの方法のノンパラメトリック版ともいえる、スティール=ドゥワスの多重比較検定 Steel-Dwass’s multiple comparison testを用いた多重比較検定について、いつも通りエクセルで算出する方法に関して説明していきます。
スティール=ドゥワスSteel-Dwass法とは?
スティール=ドゥワス検定の特徴は、ノンパラメトリックのデータを多重比較する際に用いることができる手法です。
それ以外の方法として、マン・ホイットニーU検定やウィルコクソンの符号付き順位和検定を用いて、それぞれの群を検定し、そこから多重比較検定(ボンフェローニなど)を用いる方法もあります。
それぞれの多重比較法のメリットデメリットについては以前の記事を参照してください。
エクセルでSteel-Dwass法による多重比較検定をする方法
スティール=ドゥワスSteel-Dwass法をエクセルで求める場合、以前記事にしたTukey法と同じく、統計量が有意な差といえるかどうか、有意水準の表(5%水準または1%水準)で判断します。
では実際に算出していきます。
A群~C群の3群、各群のデータ数Nは5です。
この各群のN数が一致していない場合、今回紹介するスティール=ドゥワスSteel-Dwass法をエクセルで求めるのはかなり面倒なので、その場合は統計ソフトを用いることをおすすめします。
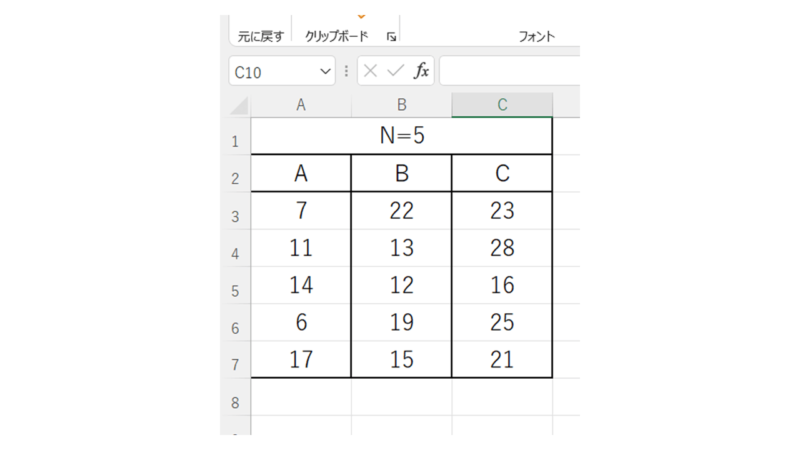
ノンパラメトリック検定なので、まずはこれらを順位(rank)処理していきます。
A-B、A-C、B-Cの3通りに対して、比較する2群でデータを昇順もしくは降順で並べ、順位をつけていきます。
※同順位の場合はマンホイットニーの時と同様の処理をします(例:9位が同順位なら9.5など)

データに順位を付けて並べ直したらその順位の数値を合計(SUM関数で算出)します。
A-BではA群の順位の合計は20です。
このとき2群の内、どちらか一方の群の順位を合計すればOKです。
次にSteel-Dwass法に必要な統計量を算出します。
まずは期待値、Eを算出します。
C列24番、「E」の算出式
E= N数 × (2×N数+1)/2
で求めます。
今回のデータ、N数は「5」なので、
E=5(25+1)/2
=27.5
となります。

次に分散、Vを算出します。
C列25番、「V」の算出式
=N数×N数×(2×N数+1)/12
で求めます。
※ここで用いている「12」は,どのような場合でも関係なく12です。
今回のデータ、N数は「5」なので、
V=55(2*5+1)/12
=22.92
となります。
E=27.5、V=22.92、この2つを用いて各群の比較した統計量を算出します。
各群の順位合計から期待値を差分したものの絶対値を分散のルートで割ります。

今回の場合、A群とB群の場合は
A-B:=ABS(B8-B23)/SQRT(B24)
となります。
他の組み合わせも同じように求めていきます。
A-C:=ABS(B15-B23)/SQRT(B24)
B-C:=ABS(B22-B23)/SQRT(B24)
ここで算出した数値から有意かどうかを判断しますが、その数値は【スチューデント化された範囲の表】を用います。
以下にスチューデント化された範囲の表(5%水準と1%水準の表)を置いておきます。
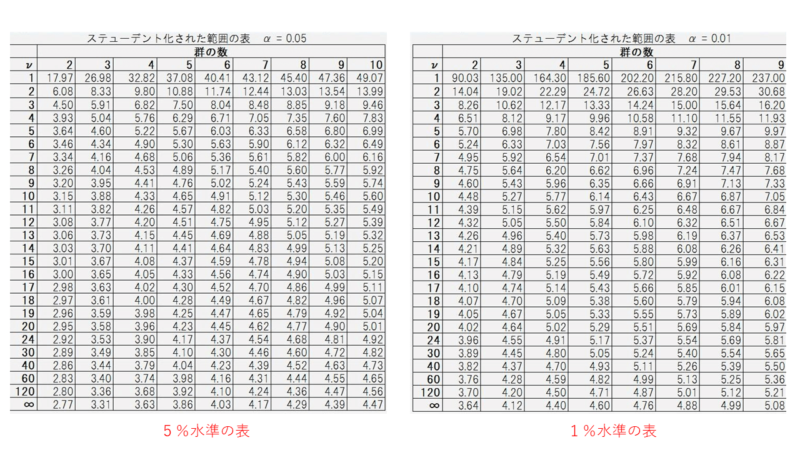
ここで用いる数値は、群の数とνが∞の部分になります。
今回は3群なので、3群と∞の部分を用いますので、5%水準の表では「3.31」ということになります。

この「3.31」をルート2で割ります。
=3.31/SQRT(2)
=2.341
この数値より、先ほど求めた各群の比較統計量の数字が大きい場合、有意性が認められると判断します。
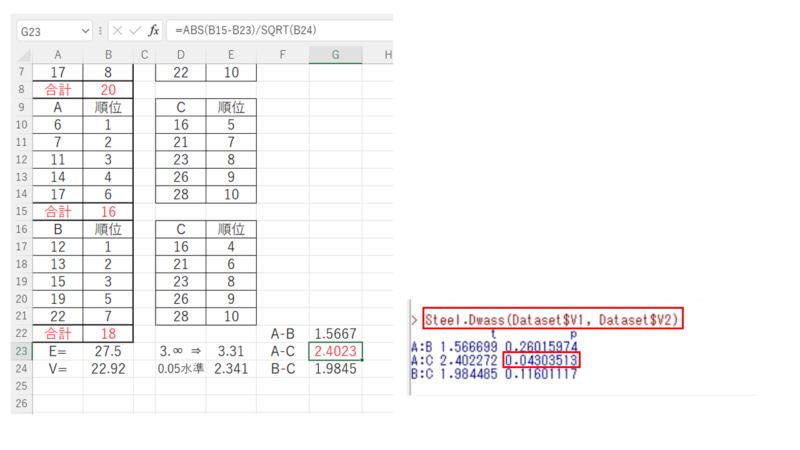
今回のデータではA群とC群の比較に有意性が認められました。
確認のため、無料統計ソフトEZRで算出、同様の結果になりました。間違いなさそうです。




コメント