前回はノンパラメトリックで対応のある2群間のデータの時に使う検定の一つ、ウィルコクソン(Wilcoxon)の符号付き順位和検定を説明しました。
今回は前回の記事でも少し触れた、似たような名前の統計手法、ウィルコクソンの順位和検定(マン・ホイットニー(Mann-Whitney)のU検定)という統計手法について、エクセルでの算出方法とともに説明していきます。
マン・ホイットニーU検定とウィルコクソン符号順位和検定の違いは?
前回も触れましたが、ウィルコクソンの順位和検定(マン・ホイットニーのU検定)とウィルコクソンの符号順位和検定、2つの統計手法の共通点と相違点を説明すると、どちらの手法も2群のデータ間における中央値の差を検定する手法ですが、相違点としては
ウィルコクソンの符号順位和検定は2群間のデータに対応があり母集団がノンパラメトリックの時に用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は対応のない2群のデータで、母集団がノンパラメトリックの時に用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)とは?
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は、対応のない2群のデータで、母集団がノンパラメトリックの時に用いるものです。
対応のある/ない、パラメトリックとノンパラメトリックの違いなどに関しては以前の記事を参照してください。
で、似たような名前の統計手法、ウィルコクソンの符号順位和検定という統計手法についても気になる方は、以前の記事を参照ください。これらは別物です。
ウィルコクソンの符号順位和検定は2群間のデータに対応がある、母集団がノンパラメトリックの時に用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は2群のデータに対応のない、母集団がノンパラメトリックの時に用います。
エクセルでマン・ホイットニーのU検定を算出してみよう!
ここからは実際にエクセルを使ってマン・ホイットニーのU検定を算出していきます。
使うデータは以下の通りです。
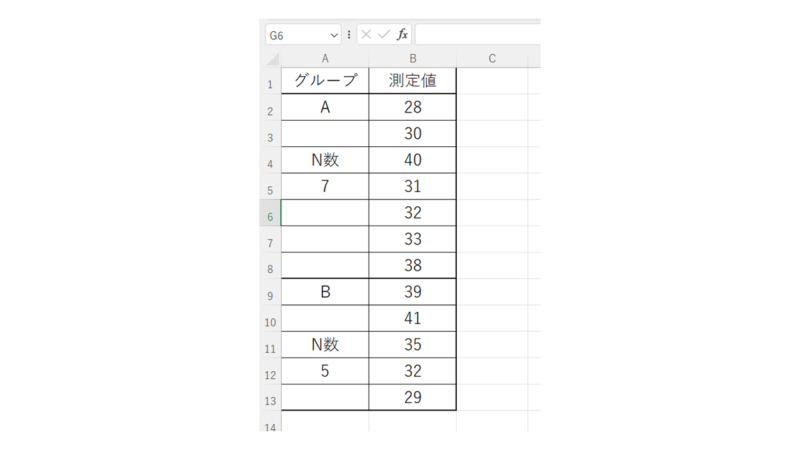
今回はA群:7、B群:5とあえて、それぞれのN数(データ数)を変えてみました。
さらにこの手法では、A群、B群、別々にではなく、まとめて順位付けをするため、見やすいように群を縦に並べておきます。
まずはA群、B群、まとめて順位付けします。
ここではRANK.AVE関数を使用します。
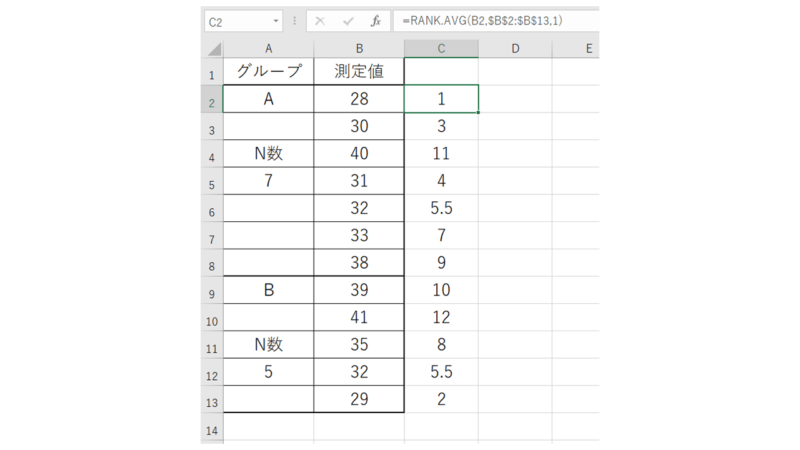
前回記載したように、RANK関数を使用した場合の注意点として、同順位が出た時です
もし、同順位が1位と2位の場合は「1.5」、2位と3位の場合は「2.5」となります。
RANK.AVE関数を用いた場合はこの操作の必要はありません。自動で平均をとってくれます。
この順位値をそれぞれの群(例ではA群とB群)で別個に合計します。
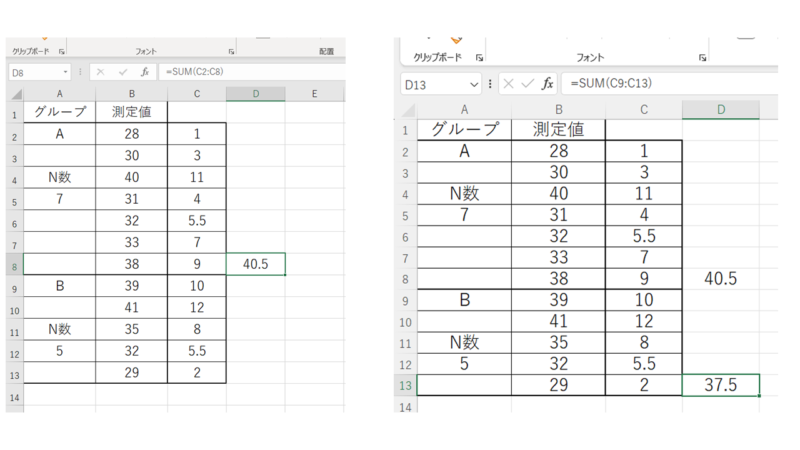
ここからマン・ホイットニーのU検定の統計量「U」を求めます。
ここでN数と合計値を使用するのですが、注意点として、A群、B群のどちらのN数や合計値を使ってもいいというわけではありません。
仮にですがN数が小さい方の群をX、大きい方の群をYとすると、算出式は
= (n数X× n数Y) + (n数X × (n数X + 1) / 2) -合計値X
となります。
実際の計算は下図の通りです。
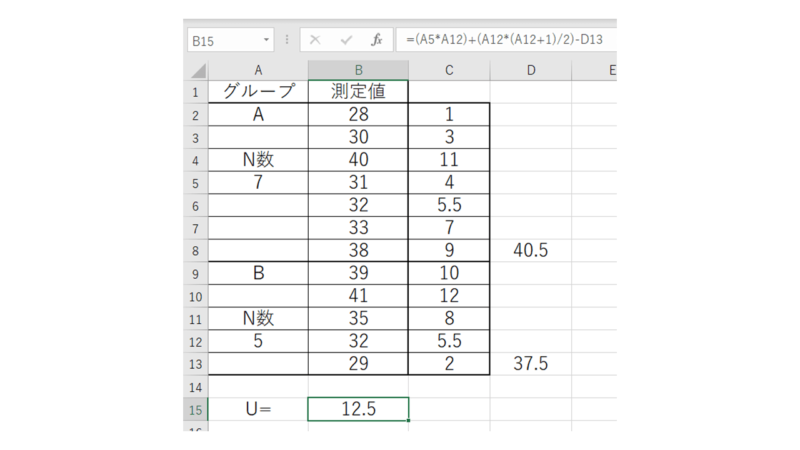
データに同順位がなければ、Uを計算して棄却限界値と比較して終了でもOKです。
U<=棄却限界値なら両群に有意差がある。
U>棄却限界値なら両群に有意差があるとはいえない。
今回は同順位がありますのでZを求め、そこからp値を算出していきます。
まずUの平均を算出します。
=n数X× n数Y/2
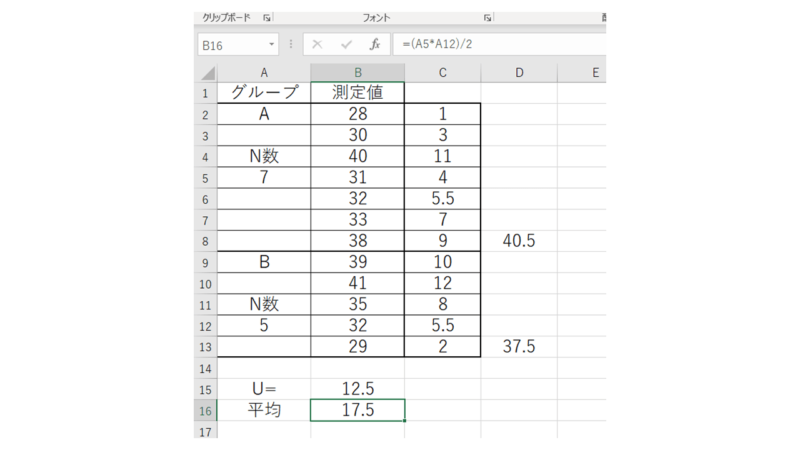
次にUの分散を出します。
先ほどと同様にN数が小さい方の群をX、大きい方の群をYとすると
=(n数X× n数Y)×(n数X+n数Y+1)/12
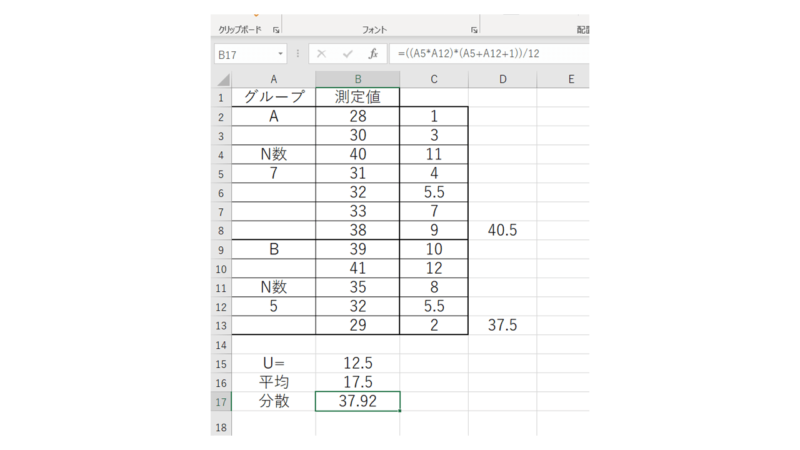
最後に「Z」を出します。
Z=|U-Uの平均|/√Uの分散
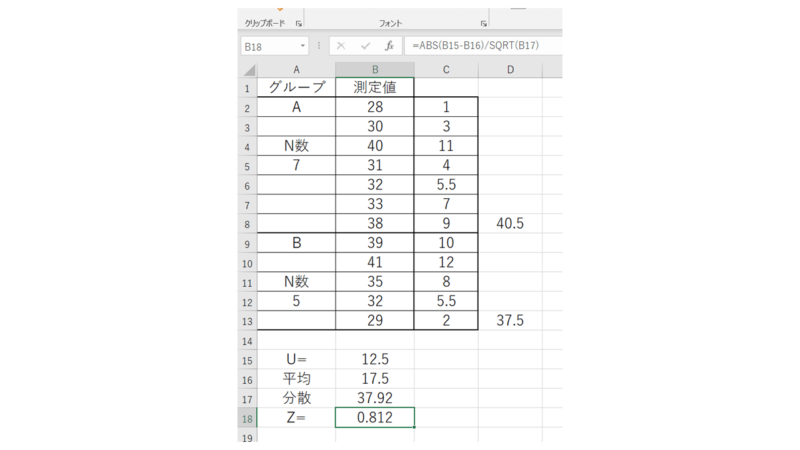
この算出した「Z」を使ってp値を算出(NORMSDIST関数を使用)します。
=(1-NORMSDIST(B17))*2
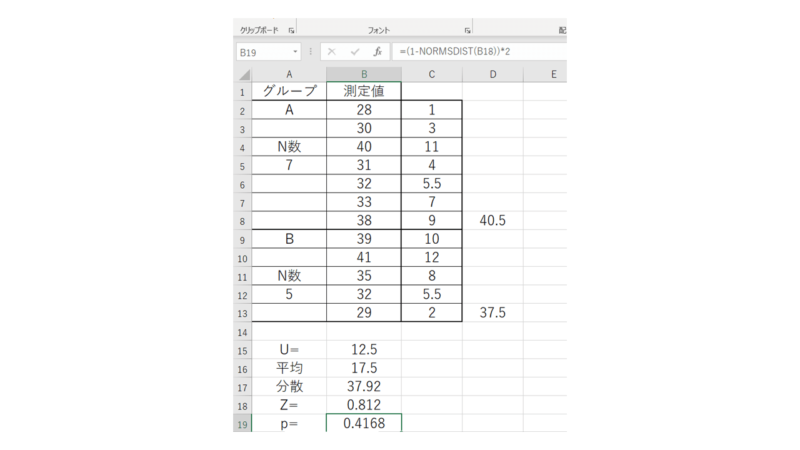
p値が算出できました。
確認のために統計ソフトで算出したp値も同じ結果になっています。
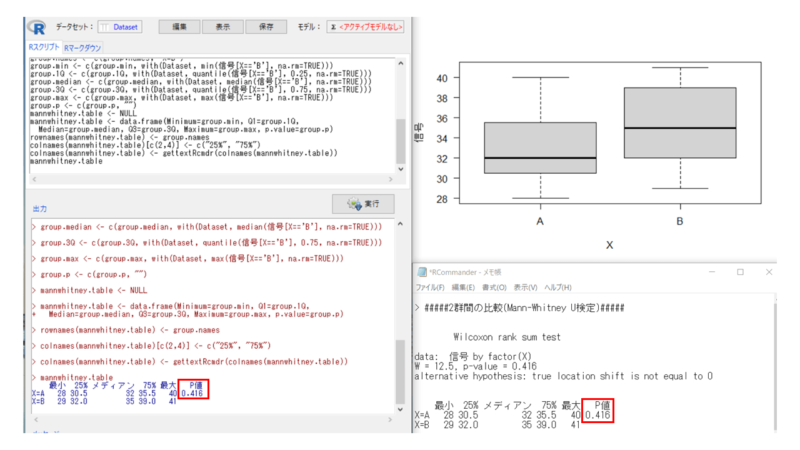
※ここでもう一つ注意点。この方法は「Z」を元に「漸近有意確率」を算出しています。
もし統計ソフトなどで「漸近有意確率」と「正確有意確率」両方の結果が算出された場合、「正確有意確率」の方が優先されるようです。
そのため、p値が0.05付近の値だった場合、「漸近有意確率」と「正確有意確率」で有意差があったりなかったりすることもあり得ます。(例として漸近有意確率は0.048、正確有意確率は0.051など)
基本的には正確有意確率の方を算出したほうが良いみたいですが、正規分布に近似させたこの手法でも間違いではないので、質問されたら(されないと思いますが)そのあたりも説明しましょう。
対応のないノンパラメトリックの2群間データに用いよう!
ウィルコクソンの順位和検定(マン・ホイットニー(Mann-Whitney)のU検定)は対応のない2群のデータで、母集団がノンパラメトリックの時に用いるものです。
ウィルコクソンの符号順位検定は、対応のある2群のデータで、母集団がノンパラメトリックの時に用います。
この2つの違いをきちんと認識し、データに適した統計手法を選択しましょう。







コメント
とても参考になりました。ありがとうございました。
ただ、最初の図では、B4セルが「39」ですが、次からは、「40」になっています。
また、横に2つ並んだ図の右側のB群の順位和計算式が誤っています。
Uを求める計算式にも誤りがあります。
ご指摘ありがとうございます。修正いたしました。