これまでEZRで対応のあるt検定、対応のないt検定、外れ値などをEZRで算出する方法を記事にしました。
今回はマン・ホイットニー(Mann-Whitney)のU検定(ウィルコクソンの順位和検定)をEZRで算出する方法を説明していきます。
エクセルでマン・ホイットニーU検定(ウィルコクソンの順位和検定)を算出する方法に関しては以前の記事を参照してください。
マン・ホイットニーのU検定とウィルコクソンの符号順位検定の違いは?
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)とウィルコクソンの符号順位検定、2つの統計手法の共通点と相違点を説明すると、どちらの手法も2群のデータ間における中央値の差を検定する手法ですが、ウィルコクソンの符号順位検定は2群間のデータに対応があるときに用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は対応のない2群のデータで、母集団がノンパラメトリックの時に用います。
マン・ホイットニーのU検定(ウィルコクソンの順位和検定)とは?
マン・ホイットニーのU検定は、対応のない2群のデータで、母集団がノンパラメトリックの時に用いるものです。
対応のある/ない、パラメトリックとノンパラメトリックの違いなどに関しては以前の記事を参照してください。
で、ここで注意点ですが、似たような名前の統計手法に、ウィルコクソンの符号順位検定という統計手法がありますが.これらは別物です。
2つの統計手法の共通点と相違点を説明すると、どちらの手法も2群のデータ間における中央値の差を検定する手法ですが、ウィルコクソンの符号順位検定は2群間のデータに対応があるときに用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は対応のない2群のデータで、母集団がノンパラメトリックの時に用います。
EZRでマン・ホイットニーのU検定を算出してみよう!
ここからは実際にEZRを使ってマン・ホイットニーのU検定を算出していきます。
使うデータは以前エクセルでマン・ホイットニーのU検定を行ったものを使用します。
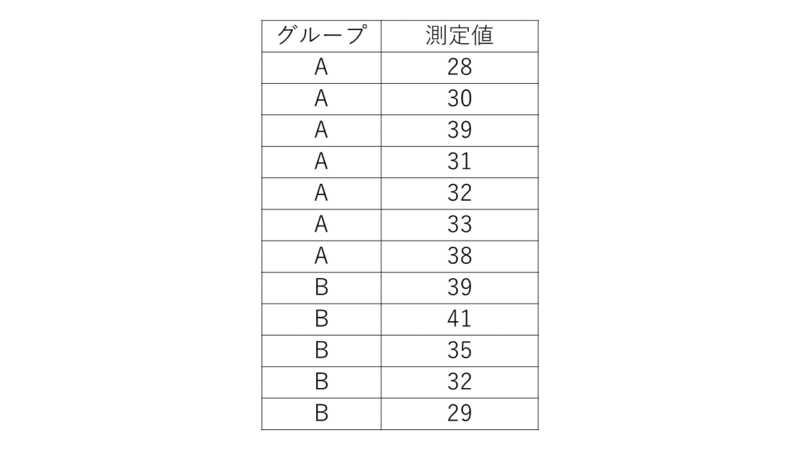
では、実際に操作をしながら順に説明していきます。まずデータを下図のように変更します。
※以前の記事でも記載していますが、対応のある時のデータ配置と、対応のない時のデータ配置の違いは、きっちり押さえておきましょう。
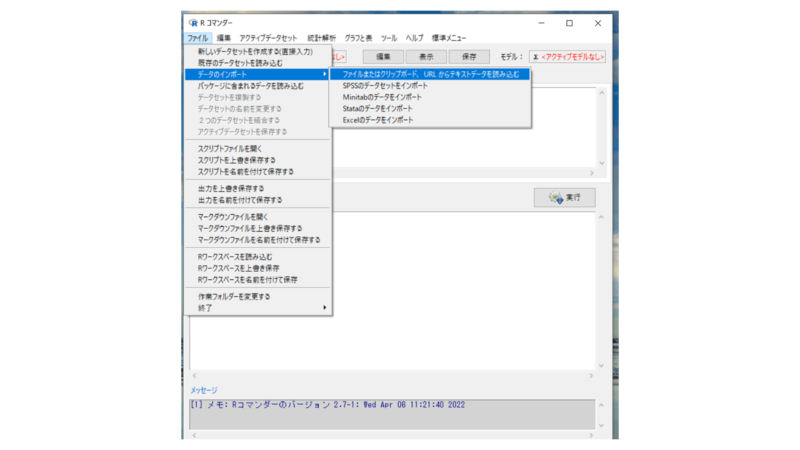
次にデータを読み取ります。「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選びます。
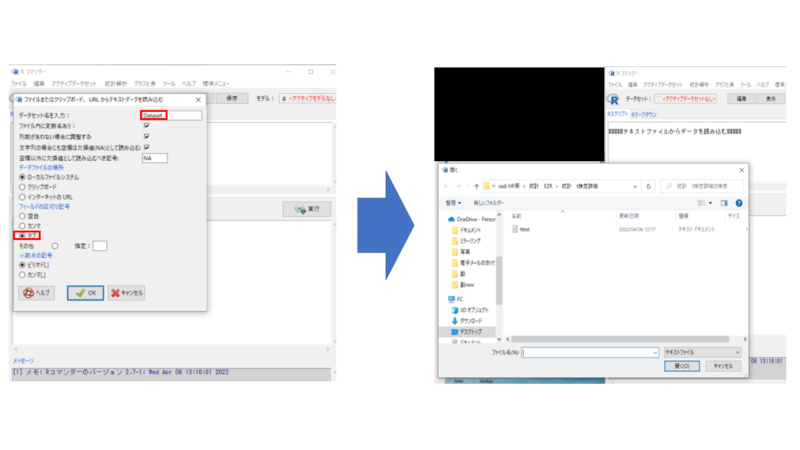
この時データセット名(赤枠)はなんでも大丈夫です。今回はそのままにしておきます。
もしクリップボード、もしくはテキストを読み込む場合は下図のように(赤枠)、カンマではなくタブを選択しましょう。
読み込みが終わったら、正常に読み込めているか確認します。
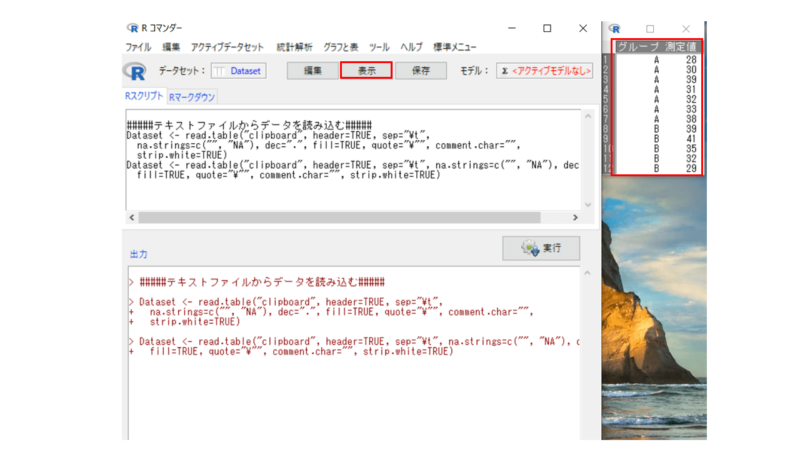
データセットの部分が、先ほど変更した名称になっているか確認し、その後「表示」を選択します。表示されたデータが正しければOKです。
データを解析していきます。今回は対応のないパラメトリックデータなので、
「統計解析」→「ノンパラメトリック検定」→「2群間の比較(マン・ホイットニーU検定)」を選びます。
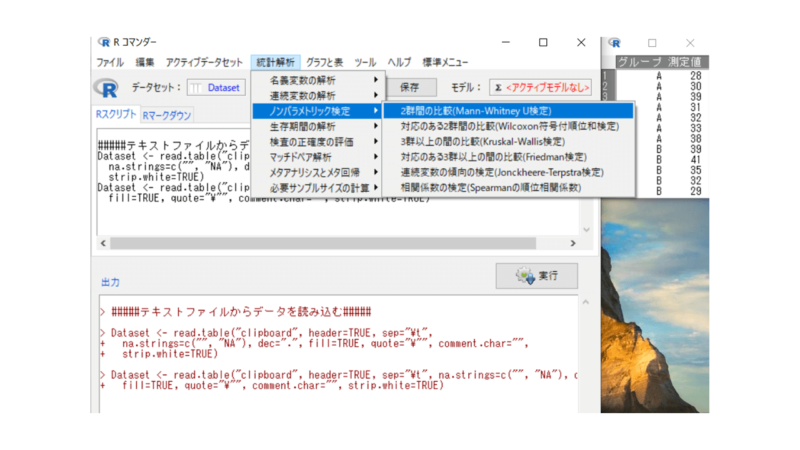
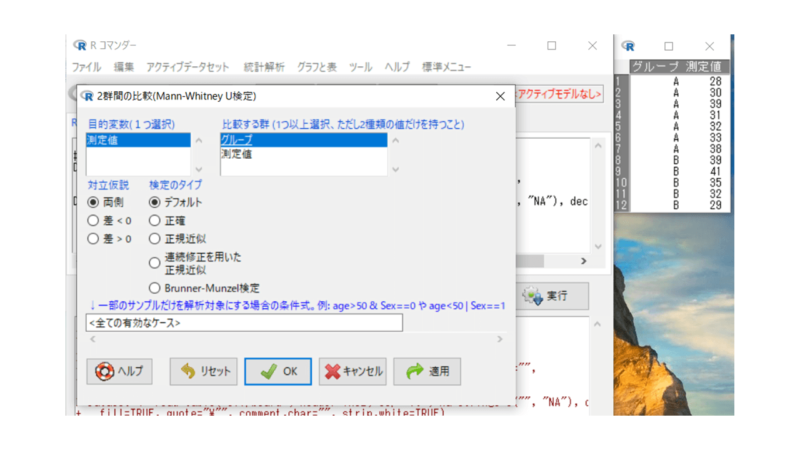
目的変数(1つ選択)で「測定値」を、比較する群(1つ以上選択)で「グループ」を選択します。
対立仮説は「両側」を、検定のタイプは「デフォルト」、他はそのままでokです。
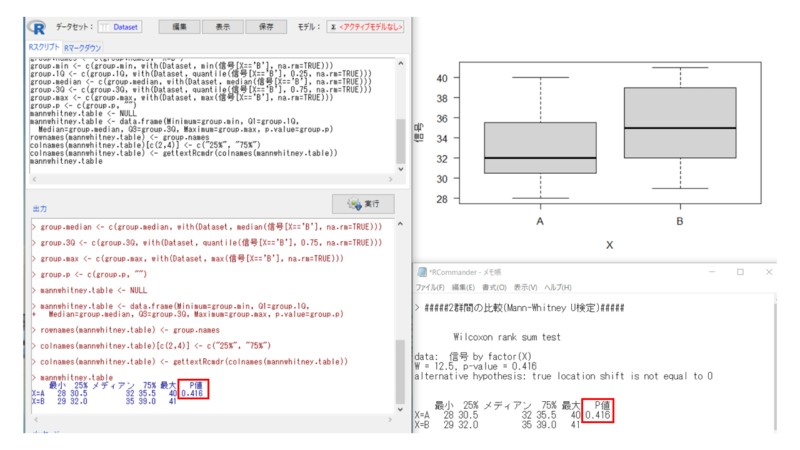
p=0.416、p>0.05となり、有意差なしと判断されます。
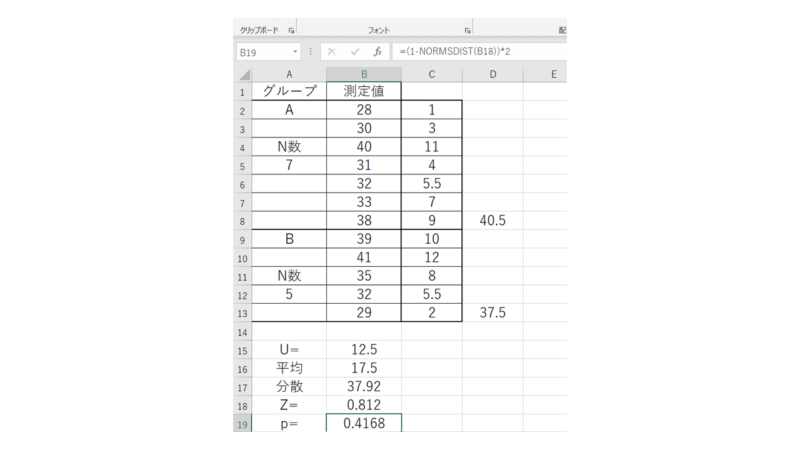
以前エクセルで求めた結果と同じになりましたので間違いなさそうです。
データの配置と解析結果の確認はしっかりと!
無料統計解析ソフトEZRは、統計解析の種類によってデータ配置が決まっています。それぞれの統計解析に合ったデータ配置を覚えておきましょう。
また、EZRで求めた値があっているか、間違っていないかをエクセルなどで解析、算出した結果と比較し、ダブルチェックすることをおすすめします。





コメント