これまでパラメトリックとノンパラメトリックの違い、対応のある/なし、エクセルでできるt検定に関して記事にしてきました。
今回はノンパラメトリックで対応のある2群間のデータの時に使う検定の一つ、ウィルコクソン(Wilcoxon)の符号付き順位和検定をやります.
ウィルコクソンの符号順位検定とは?
ウィルコクソンの符号順位検定は、対応のある2群のデータで、母集団がノンパラメトリックの時に用いるものです。
対応のある/ない、パラメトリックとノンパラメトリックの違いなどに関しては以前の記事を参照してください。
で、ここで注意点ですが、似たような名前の統計手法にウィルコクソンの順位和検定(マン・ホイットニー(Mann-Whitney)のU検定とも言う)という統計手法がありますが.これらは別物です。
2つの統計手法の共通点と相違点を説明すると、どちらの手法も2群のデータ間における中央値の差を検定する手法ですが、ウィルコクソンの符号順位和検定は2群間のデータに対応があるときに用います。
ウィルコクソンの順位和検定(マン・ホイットニーのU検定)は対応のない2群のデータで、母集団がノンパラメトリックの時に用います。
エクセルでウィルコクソンの符号順位検定を算出してみよう!
ここからは実際にエクセルを使ってウィルコクソンの符号順位検定を算出していきます。
例として、同一グループ患者群に対し、2つの治療法の前後を想定したものを作成しました。
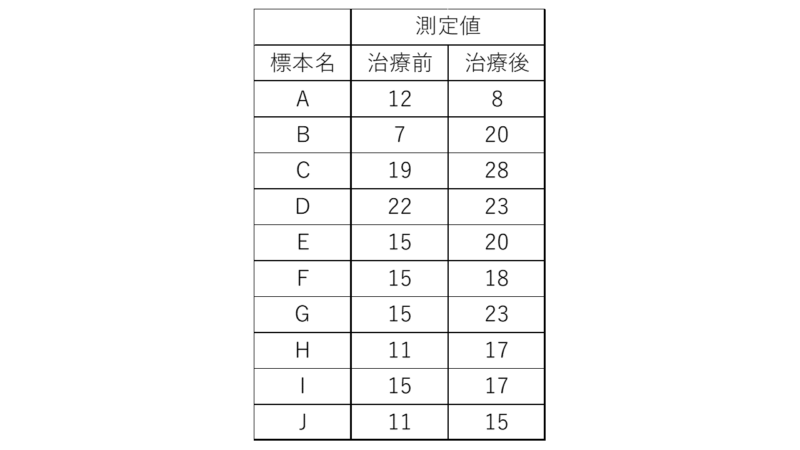
以前のt検定の記事でも書きましたが、対応のあるデータの場合、データの並べる順番には気をつけましょう(隣り合うデータは「対応がある」状態にする)。
まず、データの差を算出します。
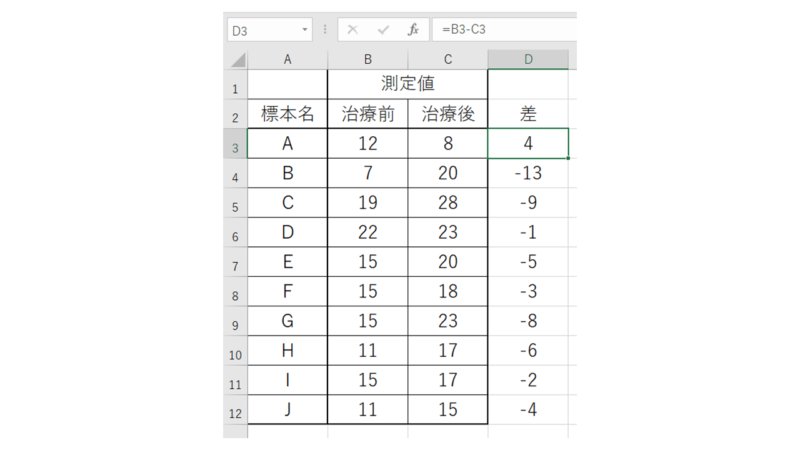
次に、求めた差に対し、ABS関数を使って絶対値にします。
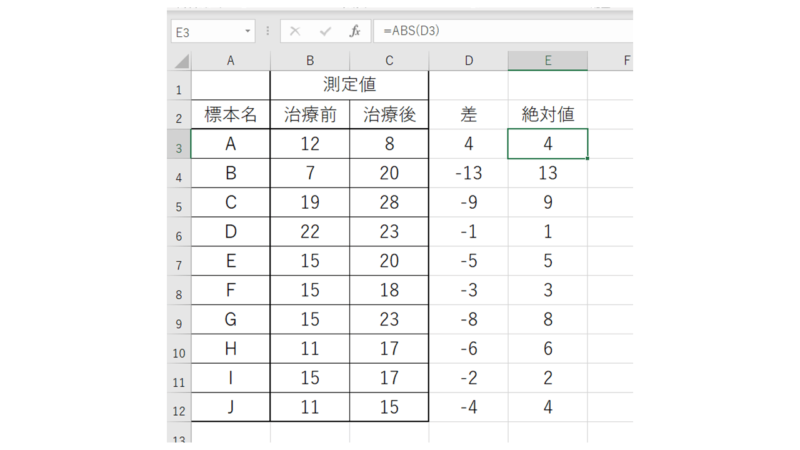
この絶対値にした数列に対して、RANK関数もしくはRANK.AVE関数を使って、昇順で順位を付けます。ここではRANK.AVE関数を使用します。
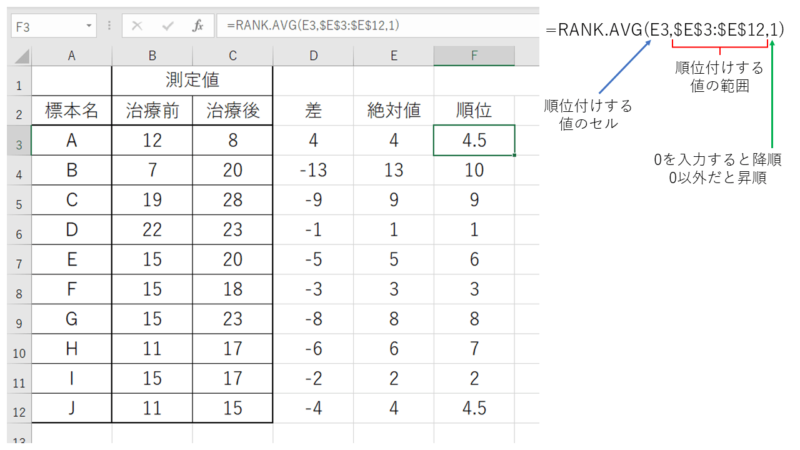
ここでRANK関数を使用した場合の注意点として、同順位が出た時(この場合だと4位が2ヶ所:AとJの値)です。例では4位と5位にあたる部分なので、この2ヶ所の「4」を「4.5」にします。もし1位と2位の場合は「1.5」、2位と3位の場合は「2.5」となります。
RANK.AVE関数を用いた場合はこの操作の必要はありません。自動で平均をとってくれます。
順位を付けたら符号付けをしていきます。
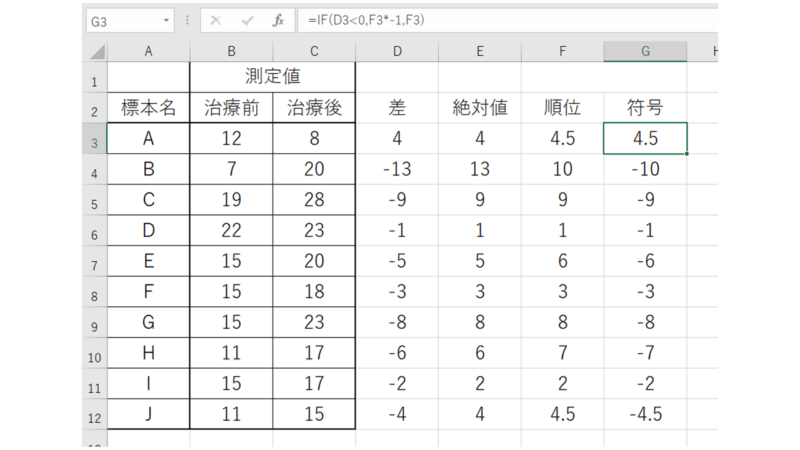
手動でも構いませんが、IF関数を使うとデータの変更などがあったときに楽です。
次はその順位を2乗します。
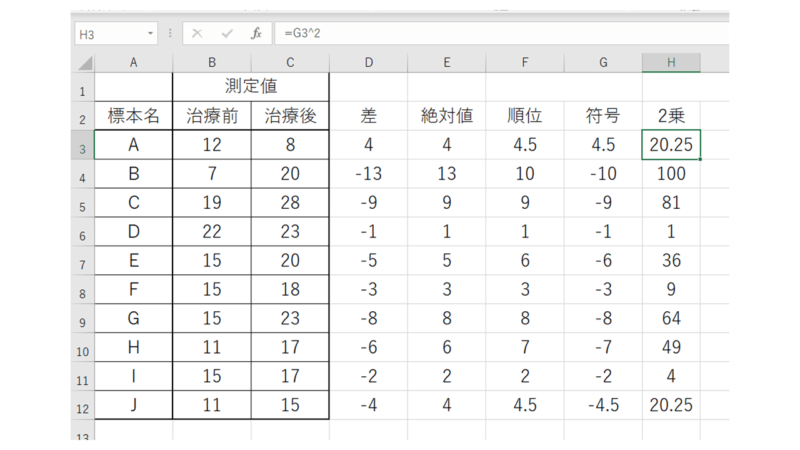
そして符号付の値の列と2乗した値の列のそれぞれの合計を求めます。
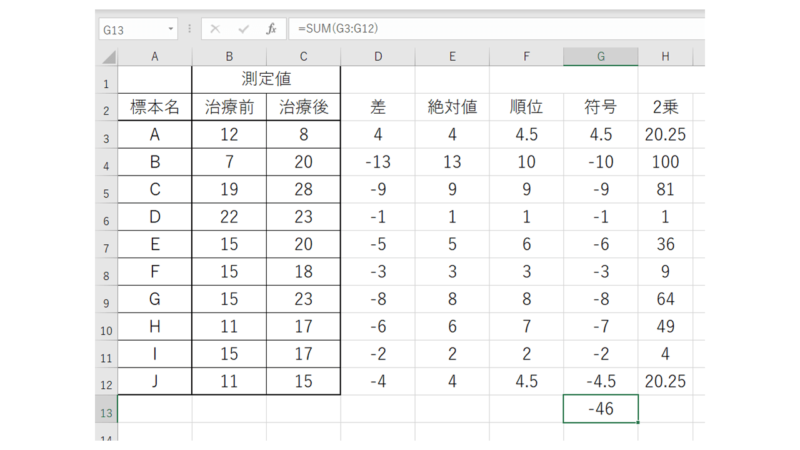
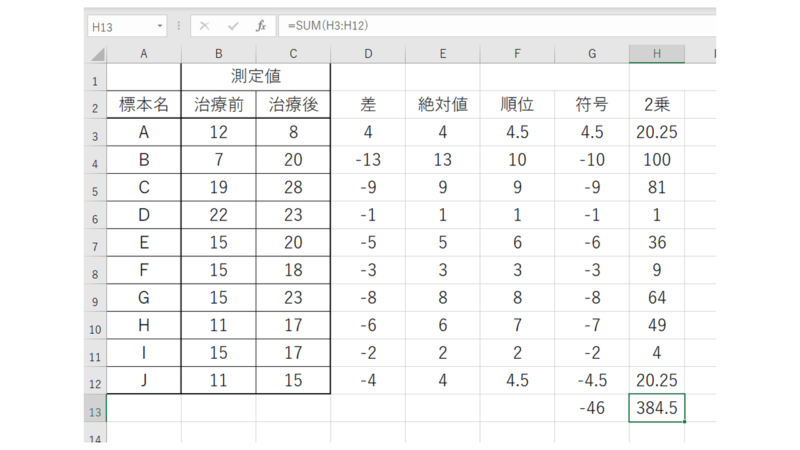
上図は符号付の列、下図は2乗の列の合計となります。
この例題では符号付の列の合計が、すでにマイナスになっているので、本来不要なのですが、この部分の値はマイナスにしておく必要があるので、説明がてら「マイナスにする」作業も入れときます。
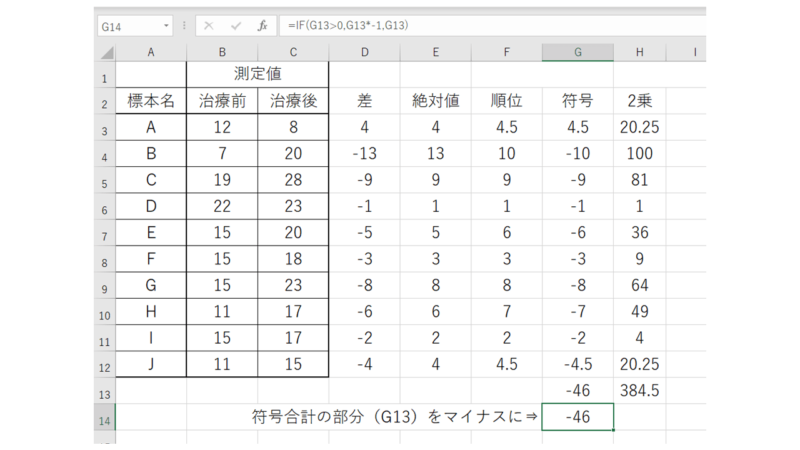
あとで元データ(治療前後データ)を変更しても大丈夫なように、IF関数を使って自動化しておきます。
ここまで来てやっと、統計量「Z」を算出できます。
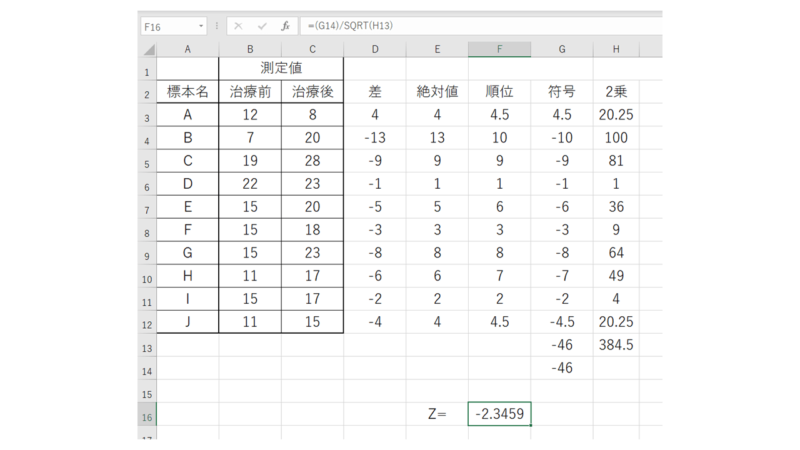
このように、マイナスにする作業を行った部分の数値(G14)と2乗の合計(H13)を使用します。
最後に「Z」を使ってp値を算出すればOKです。
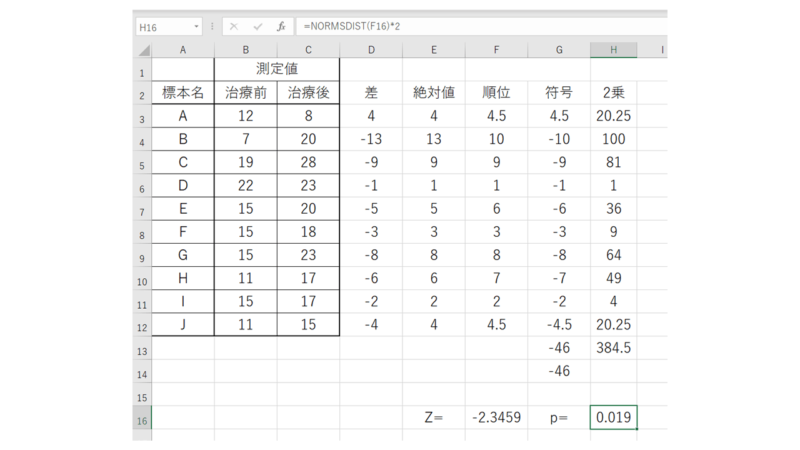
NORMSDIST関数を使います。この関数の(z)のところに,さっき出した「Z」の値を入れ、2倍します。
これで完了です。
今回の例では、p=0.019となり、対応のある2群のデータには5%水準で有意差が認められました。
確認のため、統計ソフトEZRで算出した結果(赤枠の部分)、P値=0.019になっていました。
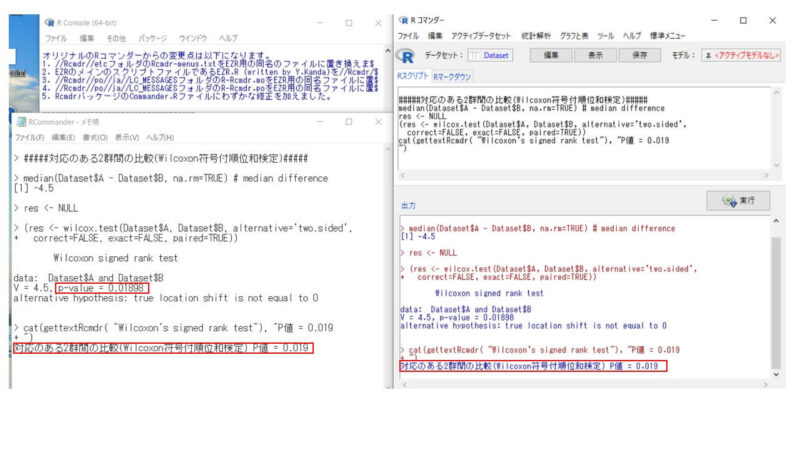
※ウィルコクソンの符号付順位和検定で注意点を挙げておくと、差がない(差が0になる)データは順位付けに用いないようにしましょう。
これで対応のある2群のノンパラメトリック検定もエクセルでできるようになりました。
対応のあるノンパラメトリックの2群間データに用いよう!
ウィルコクソンの符号順位検定は、対応のある2群のデータで、母集団がノンパラメトリックの時に用いるものです。
ウィルコクソンの順位和検定(マン・ホイットニー(Mann-Whitney)のU検定とも言う)は対応のない2群のデータで、母集団がノンパラメトリックの時に用います。
この2つの違いをきちんと認識し、データに適した統計手法を選択しましょう。
もっと統計について詳しく勉強したい!統計ソフトEZRの使い方を知りたい!という方は下記の本をおすすめします。一度機会があれば読んでみてください。






コメント