前回の記事で、3群以上のパラメトリックデータの場合、一元分散分析で有意性を確認した後に多重比較検定の一つ、ボンフェローニ:Bonferroniで検定する方法を記事にしました。
今回は3群以上の対応のあるノンパラメトリックデータに関して有意性を検定する方法であるフリードマン:Friedmanの検定について、いつも通りエクセルで算出する方法に関して説明していきます。
フリードマンの検定
フリードマンの検定は、対応のあるノンパラメトリックデータに使用するものです。
実際の算出方法のイメージとしては以前記事にしたウィルコクソンの符号付順位和検定のような検定方法です。
では実際に例のごとく適当なデータを作成して算出していきます。
データ群はA,B,Cの3群、測定回数N=5です。
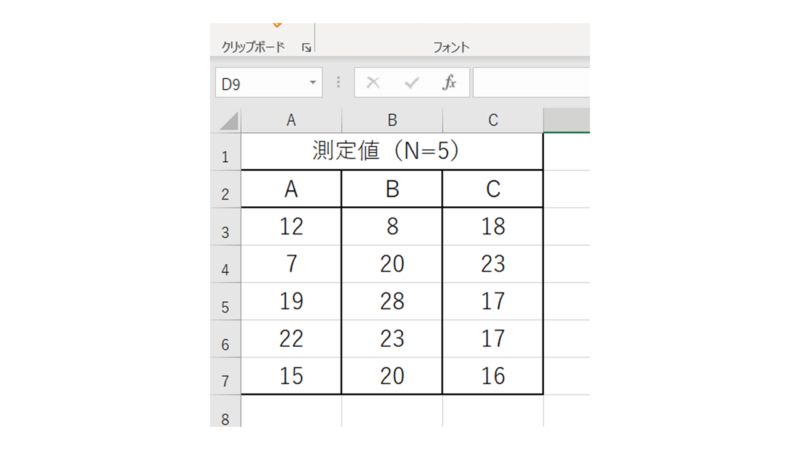
まずはノンパラメトリック検定でおなじみ、順位付けをします。ここで注意点、フリードマンの検定ではデータ郡(ここではA,B,C)で順位づけします.

こんな感じですね。全部やってしまいましょう。
※同順位値が出たら以前の記事でも書いたように、それ用の処理をしてください。
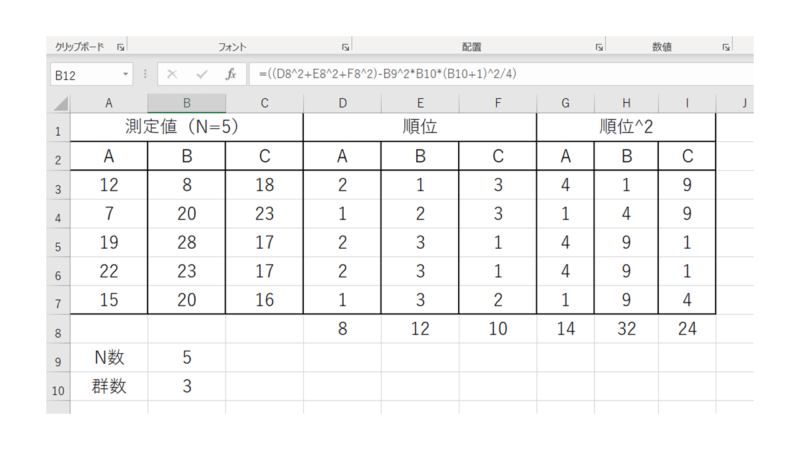
順位付けが終わったら、各順位合計を算出します。

次にウィルコクソンの符号付き順位和検定の時と同様に、順位を2乗していきます。

さらっと全部やってしまいましょう。で、こちらも合計します。

では、ここから統計量を算出していきます。
群数とN数を使いますので、計算しやすいようエクセルに置いておきます
わかりやすいようにある程度、分割して算出していきます。
まずは1つ目のT(T1)として
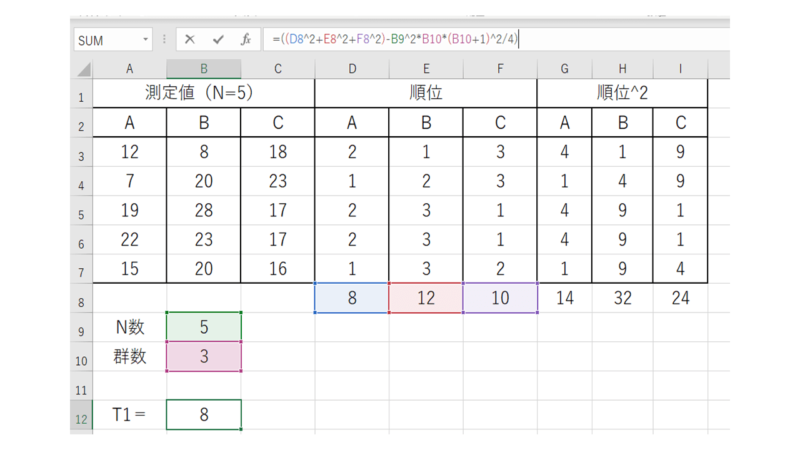
=((D8^2+E8^2+F8^2)-B9^2*B10*(B10+1)^2/4)
少しややこしいですが、これは順位の合計値と群数、N数を用いて算出しています。
次に2つ目のT(T2)として
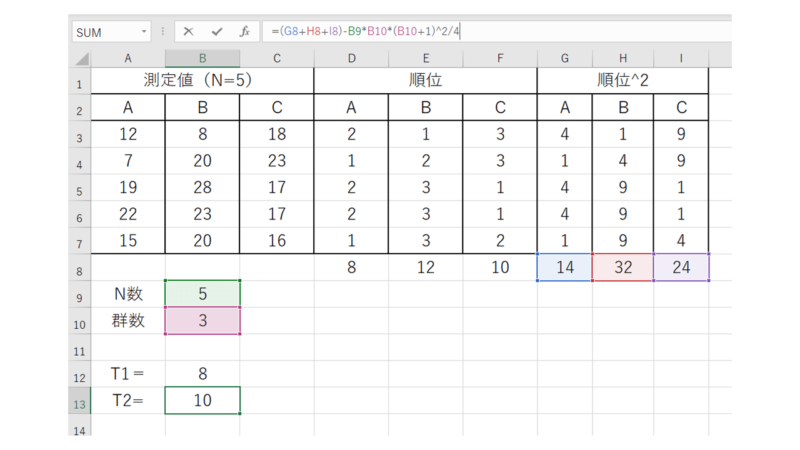
=(G8+H8+I8)-B9*B10*(B10+1)^2/4
これは順位2乗部分の合計値と群数、N数を用いて算出しています。
そして算出したT1とT2、群数を用いて統計量Tを算出します。

=(B9-1)*B11/B12
これで統計量が算出できました。
あとは統計量Tに対して、CHIDIST関数を使ってp値の算出をすればOKです。
自由度は「群数-1」なので、今回は「2」になります。
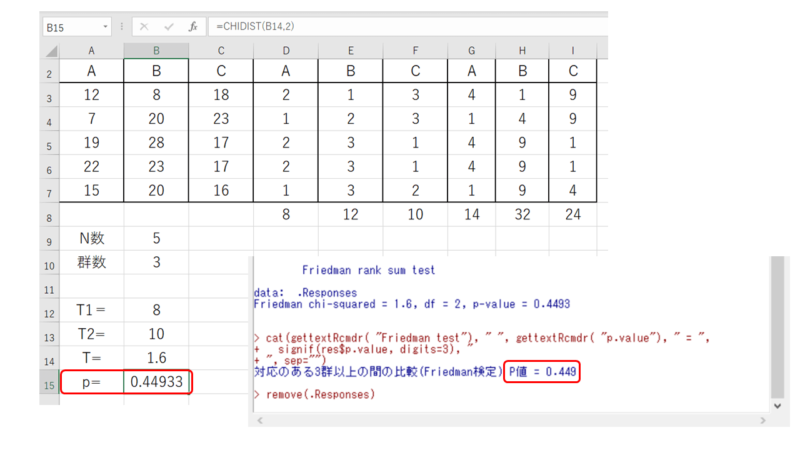
ここで有意性があれば、前回の記事のように多重統計を行いますが、今回はp値0.449なので、データの群間には有意性がないということになります。
統計ソフトEZRでも同じ結果になりました。
3群以上の対応のあるノンパラメトリックにはフリードマン検定を!
今回、3群以上の対応のあるノンパラメトリックデータの有意性を検定する方法であるフリードマンの検定をエクセルで算出する方法に関して説明しました。
同じ3群以上のデータでも対応がある、対応がない、パラメトリック、ノンパラメトリック、それぞれにおいて有意性を確認した後に多重比較検定をする必要があります。
自分の扱っているデータに合った検定を行うよう心がけましょう。




コメント