久々のエクセルで算出してみる。のシリーズは効果量(effect size)についてです。
実験結果に対し「t検定」や「分散分析」「多重比較」で統計処理しつつ、効果量も算出、記載することを推奨する学会も多々見受けられます。
効果量の算出はシステマティック・レビュー、メタ分析などでは、よく目にする統計手法ですが、
医療業界ではどちらかというと「統計的に有意」という結果でまとめられている発表、論文が多く、あまり目にすることがない方もいるかと思います。
今回の記事では、効果量の算出方法とともに、なぜ効果量を算出、記載した方が良いか、その理由に関しても説明していきます。
なぜ効果量を算出するの?
なぜそのようになっているか、という理由についてですが、t検定や分散分析などは「データが正規分布している」ことを仮定している統計手法ですが、実際の実験では、そのデータが正規分布しているかどうか確認が取れない場合もあるためです。
特に母数(N)が少ないとその傾向が顕著になります。
t検定の前提として、正規分布している(はずの)データなので、比較しているグループの平均値に差があるかどうかを「p値(probability値)」で推計しようというのが根本にあります。
するとサンプルサイズ(測定したデータの数)が少なかったりすると正規分布しているかどうかは疑わしくなり、学会発表や論文などで質問者や査読者につっこまれたりします。
それに反論するのはなかなか大変です。
なので、それに対して確率(p値)以外の方法で結果を示そう!ということで、出てくるのがサンプル数の影響を受けない「効果量(effect size)」となるわけです。
効果量(effect size)をエクセルで算出してみよう!
では実際にデータを用いて、効果量(effect size)を算出していきますが、その前にとりあえず、サンプル数も少ないですが、ひとまず正規分布していると仮定して対応のあるt検定をしてみます。
(t検定をエクセルで求めるやり方は以前の記事を参照してください)

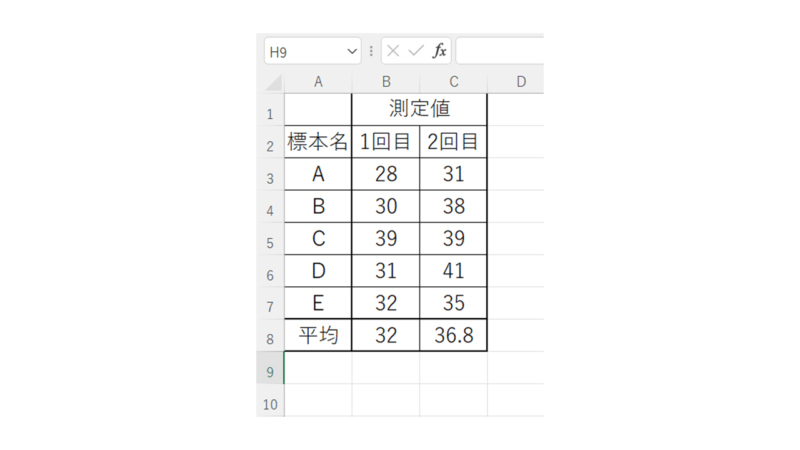
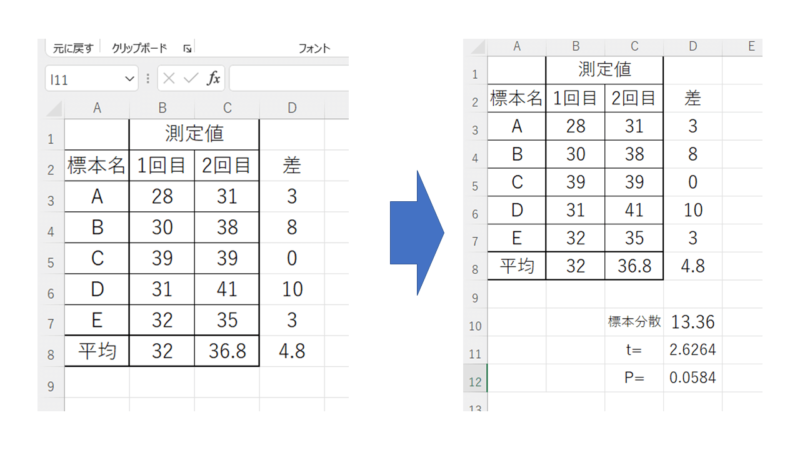
このようにt検定ではp>0.05であり、有意差が見られない結果となりました。
しかし研究内容によっては、この前後の値はある程度でも差があれば重要だという場合もあります。
そのようなときに、効果量を算出するとどうなるか計算していきましょう。
効果量の算出方法ですが、至ってシンプルで、比較したい両群の平均値を引き算し,それを標準偏差で割るというものです。式に表すと
効果量 = ( A群平均値 − B群平均値 )÷ 標準偏差
となります。
ちなみに算出時に用いる「割り算するための標準偏差」をどこから抽出するかも重要です。
基本的にコントロール群の標準偏差を使うことが推奨されているようですが、それに対しての異論もあるようです。
今回は効果量用の標準偏差(s)、「比較したい2グループの標本平均の差の標準偏差」とされるもの(Cohenが示した標準偏差)を用いて算出します。
では順を追って計算していきます。
前後のデータに対して、それぞれの標準偏差を算出し、
N数(サンプル数)、5人のデータなので5を入れます。
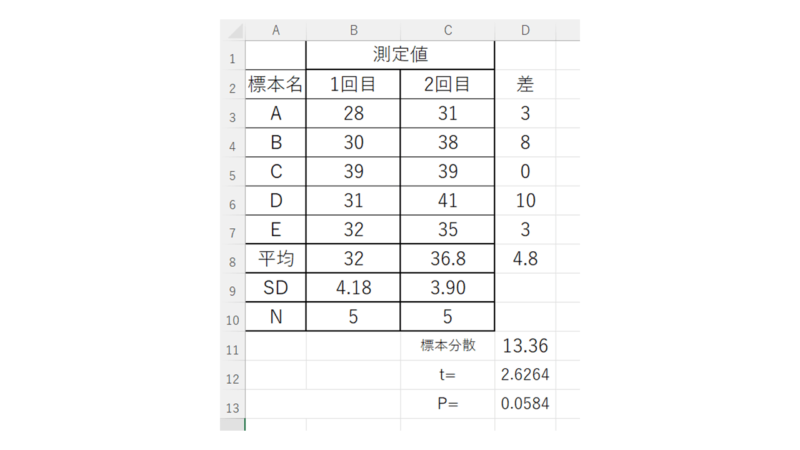
効果量用の標準偏差(s)を求めます。
算出式は
=SQRT(((B10-1)B9^2+(C10-1)C9^2)/(B10+C10-2))

効果量用の標準偏差(s)が求まりました。
これを使って効果量を計算します。Effect size (wikipedia) より効果量は絶対値で評価するので、
算出式は
=ABS(B8-C8)/D15
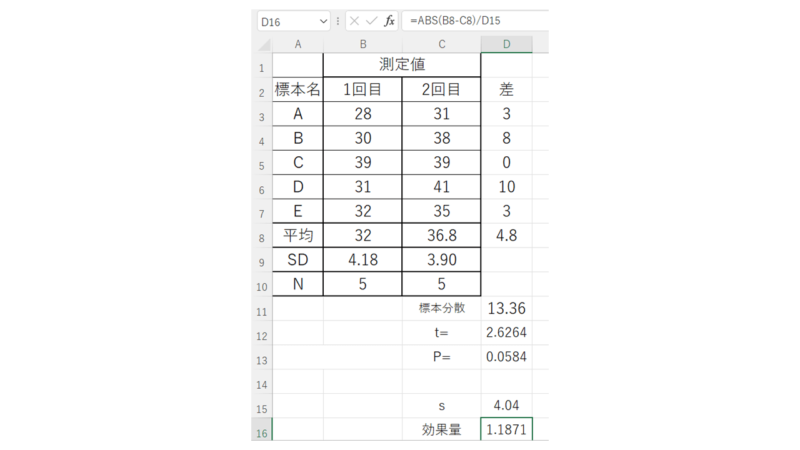
効果量が算出できました。
ではこの値はどのように解釈すればいいのか?ということですが、今回は- 1.1871の絶対値なので「1.1871」となります。
ここでEffect size (wikipedia)の表(下図参照)を見ると,効果量は「large」と「very large」の間、「very large」付近の大きさだと言えます.
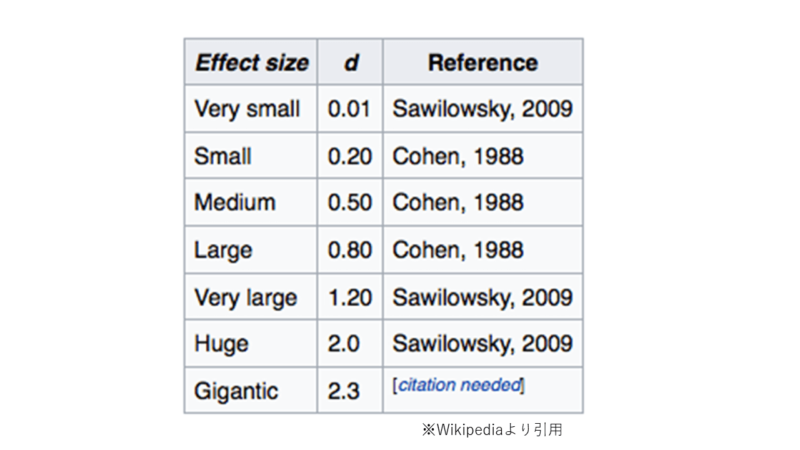
つまり,「本研究では被験者に強い効果を及ぼした」と解釈できます。
有意差検定と一緒に効果量も評価しよう!
N数が少なくて正規分布しているか確信が持てない、t検定やノンパラメトリック検定で有意差が出ない、そんな時には、効果量を算出し、2群間の差を評価してみてはいかがでしょうか。




コメント