以前の記事で、3群以上のデータを色々な多重比較検定を用いて算出する方法を記事にしました。
今回は3群以上のパラメトリックデータに関して有意性を検定する方法でよく用いられるテューキーTukey法による多重比較検定について、いつも通りエクセルで算出する方法に関して説明していきます。
テューキーTukey法とは?
Tukey法の最大の特徴は、他の多重比較法と比べて検出力が高い、すなわち検定の精度が高い手法となります。
そのため多重比較法の中でTukey法は非常によく使われています。
ただし、Tukey法を用いるには、各群の分散が等しく、各群の分布が正規分布していることが前提となります。
それ以外の場合は他の多重比較検定(ボンフェローニなど)を用いる必要があります。
それぞれの多重比較法のメリットデメリットについては以前の記事を参照してください。
エクセルでテューキーTukey法による多重比較検定をする方法
Tukey法をエクセルで求める場合、これまでに記事にしてきた他の多重比較法のようにp値を算出するのではなく、統計量が有意な差といえるかどうか、有意水準の表(5%水準または1%水準)で判断します。
では実際に算出していきます。
A群~C群の3群、各群のデータ数Nは5です。
この各群のN数は一致していないと、今回紹介するTukey法は使えませんので注意してください。
※N数が違っても計算できる方法にTukey-Kramer法があります。また暇ができれば記事にしたいと思います。
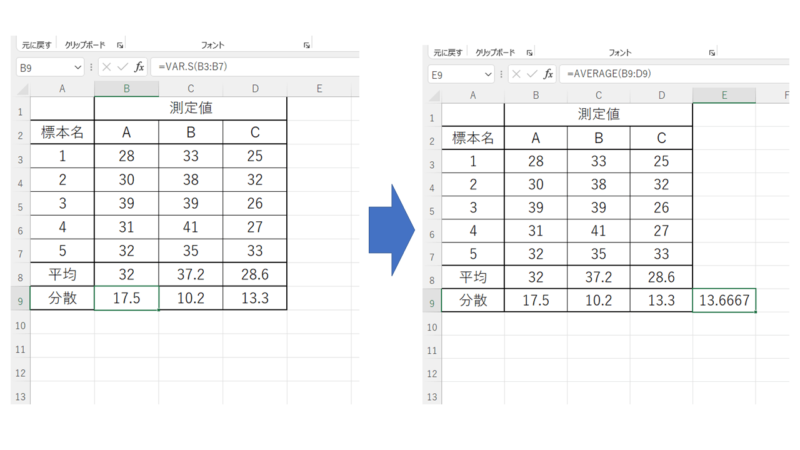
各群の平均値(AVERAGE関数)と分散(VAR.S関数)そして分散の平均もそれぞれ算出しておきます。
次にボンフェローニの時のように、比較したい群ごとに以下のように入力していきます。
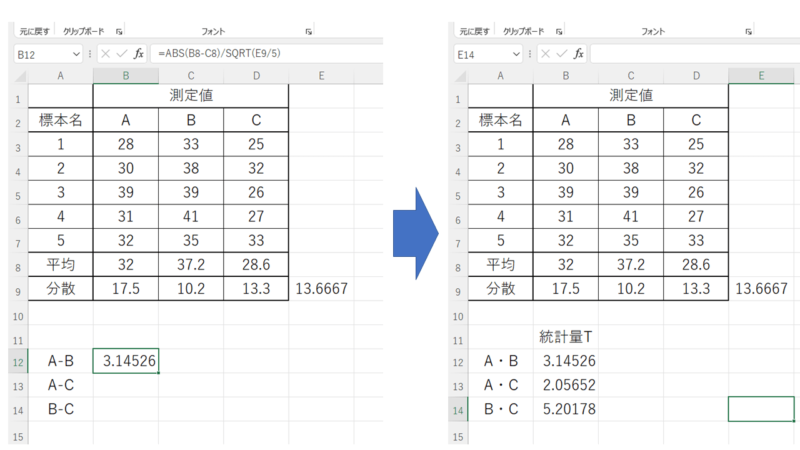
A群とB群であれば
=ABS(“A群の平均値”―“B群の平均値”)/SQRT(“分散”/”n数”)
今回の例データなら
=ABS(C8-D8)/SQRT(G9/5)
となります。
この式について簡単に言うと、比較したい群(今回はA群とB群)の平均値の差の絶対値を、「各群の分散の平均」の「13.6667」をN数「5」で割って、その平方根をとったもので割ります。
これをすべての組み合わせ(今回は3通り)で計算していきます。
これでそれぞれの組み合わせの統計量Tが算出できました。
あとはスチューデント化された範囲の表に照らし合わせて有意かどうかを判断するだけです.
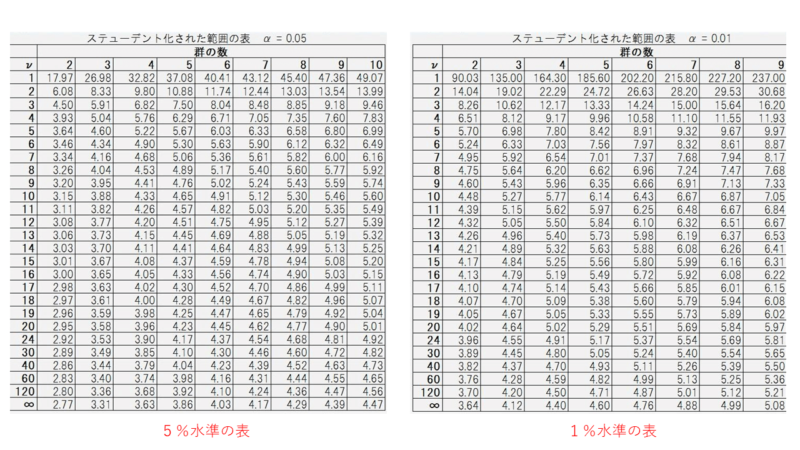
ではこれらの統計量Tが有意といえるかどうか、確認していきましょう。
今回は5%水準の方を見ていきます。
このデータは3群でNが5なので、群の数:3、ν:5の部分になりますので「4.60」です。
この「4.60」よりも統計量Tが大きい組み合わせが有意差ありとなりますので、
今回のデータで見てみると、
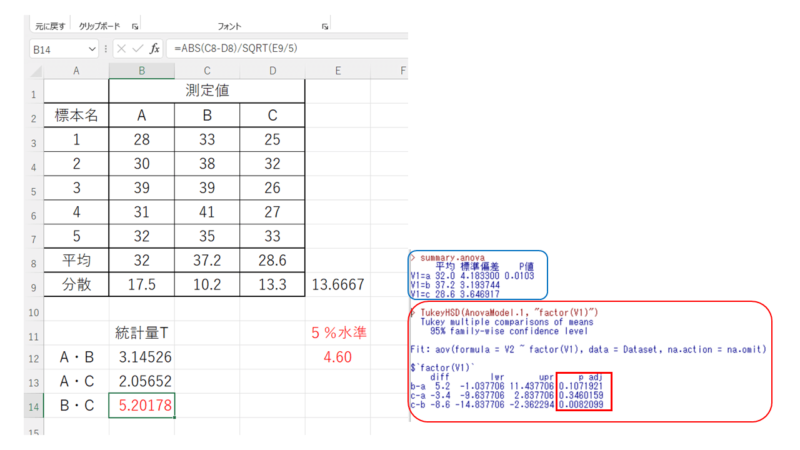
「4.60」より統計量Tが大きいB群とC群に有意差ありという結果になります。
いつものごとく統計ソフトでも同じデータで確認したところ、B-Cに有意差が認められました。間違いなさそうです。
※参考までに、このデータでボンフェローニ法(Bonferroni法)による多重比較の結果も示します。
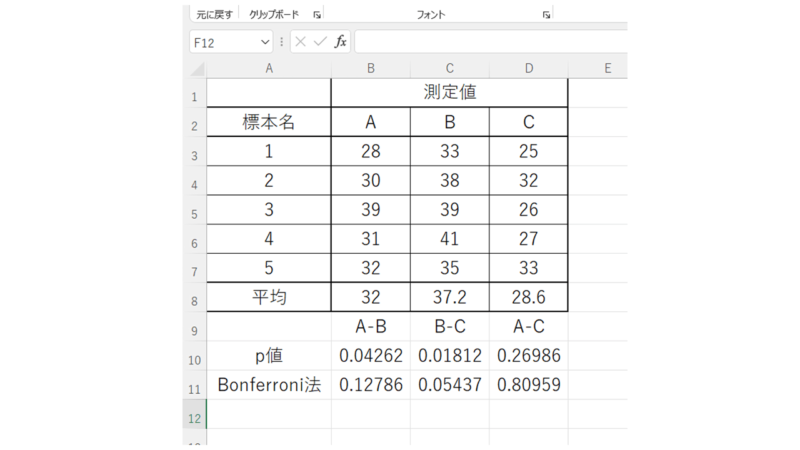
すべての組み合わせにおいてp値>0.05となり、有意差がない結果となっています。
このようにボンフェローニ法の多重比較結果と比べてみると,Tukey法の検出力が高いことがわかります。
多重比較検定の中でもTukey法はおすすめ!
前回の記事でも書きましたが、ボンフェローニ法は4群以上の多重比較になると有意性の検出が著しく低下します。
つまり「データに有意差が認められた」と結論で言いたいのに言えない、そんなときには検出力が高いTukey法がおすすめです。
多重比較法の中で最も有名な手法の一つで、論文でもよく使われていますので、統計に慣れていない方は、実験データの条件が当てはまれば(パラメトリック、各群のN数が等しい)まずはTukey法を試してみるのが良いのではないでしょうか。





コメント